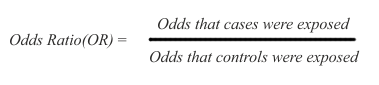Difference between revisions of "Scientific Figures"
m (→Relative Risk/Odds Ratio: spaces added) |
(→How to interpret scientific epidemiology reports?: hyphens to en-dashes) |
||
| Line 103: | Line 103: | ||
[[File:RR_CI.png|right|Example 4]]So let's have a look at some examples: | [[File:RR_CI.png|right|Example 4]]So let's have a look at some examples: | ||
| − | #RR or OR = 1.9 (95%CI 1. | + | #RR or OR = 1.9 (95%CI 1.2–4.6) means that the best estimate of the risk may be 1.9, but that its true value could be anywhere between 1.2 and 4.6, with a probability of 95% that it is indeed in that range, and a 5% possibility that the true value is actually outside that range! It also means that within that range all values are statistically significant at the 95% level, because all would mean an increase of risk, the lowest value still being >1. |
#RR or OR = 1.9 (95%CI 0.7–2.3) ) means that the best estimate of the risk may be 1.9, but that its true value could be between 0.7 and 2.3, with a probability of 95%. It also means that some values could be <1 and could mean protection, others could be >1 and could mean risk. As a consequence the result is said to be equivocal and not statistically significant. | #RR or OR = 1.9 (95%CI 0.7–2.3) ) means that the best estimate of the risk may be 1.9, but that its true value could be between 0.7 and 2.3, with a probability of 95%. It also means that some values could be <1 and could mean protection, others could be >1 and could mean risk. As a consequence the result is said to be equivocal and not statistically significant. | ||
| − | #RR or OR = 0.7 (95%CI 0. | + | #RR or OR = 0.7 (95%CI 0.2–0.9) ) means that the best estimate of the risk may be 0.7, but that its true value could be anywhere between 0.2 and 0.9, with a probability of 95%. It also means that within that range all values are statistically significant at the 95% level, because all would mean a reduction of risk, the highest value still being <1. |
| − | #RR or OR = 0.7 (95%CI 0. | + | #RR or OR = 0.7 (95%CI 0.3–1.9) means that the best estimate of the risk may be 0.7, but that its true value can only be said to be between 0.3 and 1.9, with a probability of 95%. It also means that some values could be <1 and could mean protection, others could be >1 and could mean risk. As a consequence the result is said to be equivocal and not statistically significant. |
===Confounders or co-factors=== | ===Confounders or co-factors=== | ||
Revision as of 12:16, 26 June 2012
Contents
- 1 Interpreting scientific figures
- 1.1 Epidemiologic studies of passive smoke (ETS) – not the same as science
- 1.2 Study types in epidemiology
- 1.3 Relative Risk/Odds Ratio
- 1.4 How to interpret scientific epidemiology reports?
- 1.5 Confounders or co-factors
- 1.6 Bias: Corrupting influences
- 1.7 The dubious magic of meta-analysis
- 1.8 Epidemiology – fuzzy at best
- 1.9 Recommended Reading
Interpreting scientific figures
The basic foundational drive behind modern day smoking bans can be traced to former British Chief Medical Officer Sir George Godber and his chairing of a World Health Organization conference in 1975:
The overall guideline from the panels and speakers at that conference was one advising Antismokers that to successfully eliminate smoking it would first be essential to foster a perception that would “emphasize that active cigarette smokers injure those around them, including their families and, especially, any infants that might be exposed involuntarily to ETS".
This marked the beginning of the ETS Fraud and started the true downward spiral of the quality of science as concerns smoking and health issues overall.
Epidemiologic studies of passive smoke (ETS) – not the same as science
The epidemiology of ETS (Environmental Tobacco Smoke) claims correlations of ETS exposure with cancer, cardiovascular, and other diseases that are not caused by single entities such as viruses or bacteria, but depend on a constellation of possible causes, none either necessary or sufficient. Laboratory and clinical studies have proven unable to determine specific causal mechanism for such diseases. In this regard, Doll and Peto, arguably the most prominent epidemiologists today, have concluded that:
[E]pidemiological observations ... have serious disadvantages ... [T]hey can seldom be made according to the strict requirements of experimental science and therefore may be open to a variety of interpretations. A particular factor may be associated with some disease merely because of its association with some other factor that causes the disease, or the association may be an artefact due to some systematic bias in the information collection …
[I]t is commonly, but mistakenly, supposed that multiple regression, logistic regression, or various forms of standardization can routinely be used to answer the question: “Is the correlation of exposure (E) with disease (D) due merely to a common correlation of both with some confounding factor (or factors)?”
... Moreover, it is obvious that multiple regressions cannot correct for important variables that have not been recorded at all. "…[T]hese disadvantages limit the value of observations in humans, but ... until we know exactly how cancer is caused and how some factors are able to modify the effects of others, the need to observe imaginatively what actually happens to various different categories of people will remain."[1]
(The “multiple regression” and “logical regression” referred to in the quotes above are techniques used in the statistics of epidemiology.)
Thus, while epidemiologists insist that their discipline is a science, clearly it is not the type of mainstream experimental science that produces reliable causal connections justifying public and private policies that are socially or economically injurious or disruptive.
- ↑ Doll R, Peto R, The causes of cancer, JNCI 66:1192–1312, 1981, p. 1281
Study types in epidemiology
Epidemiologic risks in general are estimated from observing differences in the frequency with which diseases appear (incidence) among groups more or less exposed to whatever agent the researchers are studying. Various types of studies are used in epidemiology, but only two have been used in the case of ETS. Let’s briefly examine how these studies are conducted, and what they actually measure.
Retrospective cohort (or longitudinal) studies
- These studies record different individual recalls of disease incidence in groups of people possibly exposed to ETS to varying degrees during the previous course of their lifetimes. In such studies, risk is estimated from differences of incidence in relation to differences in ETS exposure. Only a handful of such studies have been performed in regard to ETS.
Case-control studies
- These constitute the great majority of ETS studies. They record different individual recalls of possible lifetime ETS exposure in two groups of people. One of these groups is composed exclusively of subjects all having the disease under study (lung cancer, for instance): the subjects in this group are called the cases. The other is composed of subjects who are all free of the disease under study: the subjects in this group are called the controls.
- In case-control studies the incidence is 0% in the controls and 100% in the cases. Therefore, a key understanding is that in such studies risks are conjectured as differentials of exposure recall, and not actually estimated as differentials of disease incidence. Increased risk is inferred but not directly estimated if exposure is found to be higher among cases, and protection is inferred but not directly estimated if exposure is found to be higher among controls.
Please note that the term “individual recall” means the recollections of individual people concerning the phenomenon that the researchers are interested in. In other words, researchers in these studies use people’s memories to guess the actual amount of second-hand smoke that they were exposed to, and the comparison of the case and control groups is based on this recollection. Obviously, this fact alone is a considerable “wild card” when it comes to the reliability of the basic data upon which the study depends.
Relative Risk/Odds Ratio
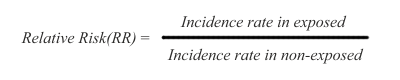
The arithmetic of risk calculation is the same for cohort and case-control studies, except for a difference in terminology. In cohort studies the ratio used for risk calculation is called RR (relative risk), while in case control studies the ratio is called OR (odds ratio).
However, the important difference is that the cohort studies estimate risk directly as differentials of disease incidence, since cohort studies observe only the health outcomes that could be associated with exposure to a particular factor. The case-control studies only assume risk from differentials of exposure, since they are designed to observe the exposure that subjects may have had in the past to the factor of interest.
Let us go into a bit more detail as to how the calculations are done – but don’t worry, it is simple arithmetic!
| Relative Risk | ||
| RR/OR | % Risk | Dec/Incr |
| 0.7 | 30% | Dec |
| 1 | 0% | - |
| 1.2 | 20% | Incr |
| 2 | 100% | Incr |
In cohort studies, risk is measured as a difference in disease incidence between exposed and non-exposed subjects. The risk is defined as relative risk (RR), and it is expressed this way:
Thus, the disease incidence rate in the exposed subjects is simply divided by the incidence rate in non-exposed subjects. The RR ratio reflects that a certain incidence of disease is observed in both non-exposed and exposed subjects, due to multiple background causes operating in conjunction with, or entirely separate from the exposure under study. Therefore, risk in the exposed is said to be an increment or decrement of incidence, relative to the basic incidence of the non-exposed subjects.
In the RR ratio above, if the rates are the same in exposed and non-exposed subjects, the RR = 1 and therefore there is no risk differential. If RR is greater than 1, the risk is said to be increased in the exposed subjects. If RR is smaller than 1, the risk is said to be decreased in the exposed subjects, indicating that the exposure under study might be possibly protective.
Because case-control studies infer but do not directly estimate possible risk, their results are expressed as odds ratios (OR), namely the ratio between the odds (expressed as % or other rate) of being exposed for the cases and the controls:
In the above ratio, if the odds are the same in exposed and non-exposed subjects, the OR = 1 and there is no inference of difference in risk. If OR is greater than 1, there is an inference of increased risk in the cases. If OR is smaller than 1, there is an inference of decreased risk for the cases, indicating that the exposure may possibly protect against the disease under study.
Both cohort and case-control studies are affected by similar difficulties of design, data collection, and interpretation — difficulties that are far worse for case-control studies that uniquely rely on vague recollections of exposure.
How to interpret scientific epidemiology reports?
| Hypothesis |
| An original assumption that must be demonstrated or rejected through experimentation. |
The reliability of any empirical evidence, scientific or not, depends on having met three basic benchmarks:
- An assurance of identity, namely that what is being measured is indeed what is claimed to be measured, and measured with sufficient accuracy.
- An assurance of the absence of other explanations, namely that the effects observed are due exclusively to what is being measured (exposure to ETS, in our case), and not to other disturbances that interfere with the observations and may alter and confound the results.
- An assurance of consistency, namely that results are consistently reproduced by different reports.
Without meeting these three guarantees, no hypothesis can aspire to reach any degree of credible evidence, and cannot be credibly taken as the basis for reasoned policy decisions, either public or private.
The important figures in a published scientific report are the Relative Risk (RR) or Odds Ratio (OR) together with the Confidence Interval (CI). The CI defines the upper and lower bounds of the published RR or OR, indicating that there is a 95% chance that the real value of the RR or OR is located beween these borders.
Scientists have defined a rule of thumb for the values of RRs or ORs:
"In epidemiologic research, [increases in risk of less than 100 percent] are considered small and are usually difficult to interpret. Such increases may be due to chance, statistical bias, or the effects of confounding factors that are sometimes not evident." National Cancer Institute, Press Release, October 26, 1994
"As a general rule of thumb, we are looking for a relative risk of 3 or more before accepting a paper for publication." Marcia Angell, editor of the New England Journal of Medicine
"My basic rule is if the relative risk isn't at least 3 or 4, forget it." Robert Temple, director of drug evaluation at the Food and Drug Administration
"An association is generally considered weak if the odds ratio [relative risk] is under 3.0 and particularly when it is under 2.0, as is the case in the relationship of ETS and lung cancer." Dr. Kabat, IAQC epidemiologist
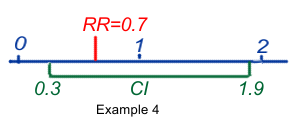
So let's have a look at some examples:
- RR or OR = 1.9 (95%CI 1.2–4.6) means that the best estimate of the risk may be 1.9, but that its true value could be anywhere between 1.2 and 4.6, with a probability of 95% that it is indeed in that range, and a 5% possibility that the true value is actually outside that range! It also means that within that range all values are statistically significant at the 95% level, because all would mean an increase of risk, the lowest value still being >1.
- RR or OR = 1.9 (95%CI 0.7–2.3) ) means that the best estimate of the risk may be 1.9, but that its true value could be between 0.7 and 2.3, with a probability of 95%. It also means that some values could be <1 and could mean protection, others could be >1 and could mean risk. As a consequence the result is said to be equivocal and not statistically significant.
- RR or OR = 0.7 (95%CI 0.2–0.9) ) means that the best estimate of the risk may be 0.7, but that its true value could be anywhere between 0.2 and 0.9, with a probability of 95%. It also means that within that range all values are statistically significant at the 95% level, because all would mean a reduction of risk, the highest value still being <1.
- RR or OR = 0.7 (95%CI 0.3–1.9) means that the best estimate of the risk may be 0.7, but that its true value can only be said to be between 0.3 and 1.9, with a probability of 95%. It also means that some values could be <1 and could mean protection, others could be >1 and could mean risk. As a consequence the result is said to be equivocal and not statistically significant.
Confounders or co-factors
Confounders are defined as hidden risk factors that could also participate in producing an association. As a general rule study subjects with cancer must, as a matter of course, have been more exposed to cancer risk factors than the healthy controls – and there are many risk factors for a disease like lung cancer that most studies either can not or simply do not control for.
For instance, ETS studies dealing with lung cancer should consider some three dozen risk factors as potential confounders reported in the literature, and studies of cardiovascular conditions face over 300 published accounts of risk factors as potential confounders. It should be apparent that without a credible control for at least all the major known confounders, epidemiologic studies of ETS could not be validly interpreted.
And even when these confounders all are taken into account, what factor was the decisive one that triggered the cancer?
Compare it with a large pot of water: if you move a lit yellow-colored cigarette lighter under it, it may never start to boil. Add a second lighter, a blue one, under it and it may boil in 100 years. Maybe after the tenth or the twentieth lighter of different colors has been lighted under the pot of water, the water will start to boil before it simply evaporates. But which lighter was the important one? None probably, as they all have worked together to heat the water. No single colored lighter could have achieved this. The red lighter might represent smoking; the blue lighter, radon; a pink lighter, automotive pollution; a green lighter, cooking fumes; and so on.
Bias: Corrupting influences
Biases are common. In simple terms, a bias is a type of error that alters the base of comparison in the study to some extent and thus “throws the results off”. When we want to compare two groups of people in an effort to get information about the possible effect of a particular factor upon them, we must start by comparing “apples with apples” as much as possible. For the sake of illustrating the point, let us imagine an extreme example of bias: the comparison of a group of eight-year-old girls with a group of 80-year-old male former prisoners of war! The differences between these groups are so extreme regarding such factors as age, life experience and medical history that almost any medical comparison between the two groups would be hopelessly compromised by the multitude of confounding factors.
A selection bias occurs when control subjects mismatch the test or case subjects in regard to characteristics that cannot be adjusted for age, gender, etc. In fact, selection bias can only be reduced, for it is impossible to eliminate. Its presence can only be guessed but not measured with any precision.
Information bias relates to inevitable inaccuracies in data collection.
Recall bias – that is, inaccurate data resulting from people’s inaccurate memories -- is most frequent, and is of special concern in case-control studies, where cases with a disease are apt to recall more intense and longer exposures to "risks" they believe may be associated with it than the controls without the disease, thus contributing to a false appearance of increased risk. Recall bias and error may be increased when exposure information is retrieved from the next-of-kin of deceased subjects. In general, recall data are based exclusively on vague individual recall statements, and no verification is possible. It is only natural that persons with cancer or other diseases would be more inclined than persons without disease to unintentionally magnify the extent of their ETS exposure, in an effort to rationalize their disease and explain it.
Differential accuracy of disease diagnostics and death certificates may also affect the classification of subjects. A misclassification bias can occur when subjects wrongly declare themselves to be non-smokers and are mistakenly classified as such. The tendency to cheat and misclassify themselves as non-smokers would be naturally more prevalent among subjects with cancer or other diseases than in control subjects that are otherwise healthy, thus contributing to a false impression of elevated risk.
Publication bias is a bias with regard to what is likely to be published, among all the research that is available to be published. Not all bias is inherently problematic, for instance, a bias against publishing lies is a good bias, but one very problematic, and much discussed bias is the tendency of researchers, editors, and pharmaceutical companies to handle the reporting of experimental results that are positive (i.e. showing a significant finding) differently from results that are negative or inconclusive (i.e. supporting the null hypothesis), leading to a misleading bias in the overall published literature. Such bias occurs despite the fact that studies with significant results do not appear to be superior to studies with a null result with respect to quality of design.
The dubious magic of meta-analysis
Meta-analysis is a statistical technique used to pool results from different studies. Originally it was developed for summarizing the results of homogeneous randomized clinical trials, a use that remains its legitimate application. However, using meta-analysis for pooling the results of diverse observational ETS studies of contrasting outcomes, of different types of subjects, with different corrections for confounders, of different sizes, in different locations, at different times, etc., etc., and thus is fraught with irresolvable difficulties.
The procedure gives different weights to studies, primarily in relation to their size. However, meta-analysis does not pool the discrete data that originated each result, but only the final results of each study regardless of whether concordant or discordant, credible or not. The procedure does not discriminate for characteristics of each study, such as design, data collection, standardizations, biases, confounders, adjustments, statistical procedures, etc. Meta-analysis, therefore, produces only a weighted average of the final numerical results of the studies, but does not standardize, relieve, or control for differential corruptions that may be present in each study. If characteristics other than study size are used in weighing studies (e.g. an estimate of study quality), those characteristics are likely discretionary, judgmental, and conducive to different meta-analysis results at the hands of different analysts.
Therefore, with the exception of its use for summarizing homogeneous randomized clinical studies, it is abundantly clear that meta-analysis can be used as a stratagem to create meaning from studies that truly have no intrinsic meaning.
Epidemiology – fuzzy at best
Indeed, numerical transformations and renditions impart an undeserved sense of accuracy and credibility to a background of vagueness caused by study design deficiencies, asymmetries in data collection, statistical error, biases, confounders, limitations of adjustments and standardizations, prejudice, and more. Tests of statistical significance are equally speculative, being no more than approximate summaries of metaphorical primary data.
| Data dredging |
| The sifting of pre-existing data from studies for the purpose of finding associations that may not have been originally made in the studies. It’s a way of recycling data to create new studies – almost instantly – at a low cost. |
More importantly, there is a general but crucial warning in reading and interpreting epidemiologic reports. Numerical displays in epidemiology should be seen as having “an analogue rather than digital” meaning. Most numbers in epidemiology are metaphorical proxies of uncertain real quantities, for epidemiology rarely measures reliably, and more commonly evokes, conceives, assesses, sizes up, adjusts, rounds up, and appraises.
As a further cautionary note, the greater the complexity of the statistical analysis in epidemiologic reports, the greater the weakness of the data is likely to be. In a practice known as data dredging, epidemiologists like to squeeze every conceivable signal out of what is usually a congeries of data.
Epidemiologists have reacted to the inherent uncertainty of their findings by adopting a vague set of causality criteria, known as the Hill criteria. However, none of the ETS studies, alone or together come close to satisfying even this vague set of criteria.
Recommended Reading
- Above selections are primarily extracts taken from Media:ETS4Dummies.pdf.
- Also read The Plain Truth About Tobacco
- Search the evidence in the Forces Scientific Portal
- The making of ETS: Lying about passive smoking
- Lies About Secondhand Smoke